Logistic, Poisson, Multinomial, and Ordinal Regression

Logistic, Poisson, Multinomial, and Ordinal Regression#

Notebook created for Regression in Psychology PSYCH–GA.2229 graduate level course at New York University by Dr. Madalina Vlasceanu

This content is Open Access (free access to information and unrestricted use of electronic resources for everyone).

Sources:

Navarro, D. (2013). Learning statistics with R: https://learningstatisticswithr.com/
Gureckis, 2018 https://teaching.gureckislab.org/fall22/labincp/intro.html

1. Logistic Regression#

Logistic Regression is a generalized linear model.
It is also called a logit model.
It is used when the DV is binary or categorical (examples: voting, correct responses, threshold based outcomes).

\[y \sim \text{Bernoulli}(p)\]

\[\log\left(\frac{p}{1-p}\right) = \beta_0+\beta_1 x\]

\[ p = \frac{1}{1+\exp(-(\beta_0+\beta_1 x))} \]

The ln(odds)= ω is called a logit.
A regression model with ω as the outcome is called logistic regression ω = B0 + B1X
The parameters of logistic regression have a natural interpretation when their antilog (exp) is taken
The constant B0 is simply the odds of the outcome when X=0
The slope B1 is an odds ratio

What is wrong with running regular ols regression on binary outcome data?

Screen Shot 2023-03-13 at 4.40.07 PM.png

The homogeneity of variance assumption of linear regression (OLS) is violated: Here the errors are not random and the same size for all values of x. Instead some errors are way larger than others:

Screen Shot 2023-03-13 at 4.44.57 PM.png

The solution is to transform the dichotomous outcome into probabilities of each of the 2 outcomes.

Example: use GPA to predict being admitted to NYU (1) or not being admitted to NYU (0). This dichotomous outcome can also be thought of as the probability (likelihood) of being admitted to NYU.

This can be achieved with the logit model.

One way to model the relationship between a continuous predictor variable 𝑋 and a probability 𝜋 is with the logistic response function, also known as a sigmoid or s-shaped curve
the logit is a function that maps the real number line to a range bounded by 0 and 1.
So the logit function takes as input any number on the real number line and converts it to a number between 0.0 and 1.0 which is handy if you want to predict probabilities

Screen Shot 2023-03-13 at 4.49.20 PM.png

Example: use GPA to predict admission outcomes:

Instead of fitting the line in the space of 𝑝(𝑎𝑑𝑚𝑖𝑡𝑡𝑒𝑑)
We will be fitting the log odds of being admitted (i.e., 𝑙𝑜𝑔(𝑝/1−𝑝)
Instead of computing residuals, we will project the data onto log odds line

Screen Shot 2023-03-13 at 4.51.21 PM.png

Examples of logistic regression models#

Probability of defaulting on bank loan given demographic characteristics

# import libraries

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.genmod.generalized_linear_model import families
from patsy import dmatrices
from statsmodels.discrete.discrete_model import MNLogit

# import data downloaded from https://github.com/mvlasceanu/RegressionData/blob/main/creditdefault.xls
# df = pd.read_excel('creditdefault.xls')

# Or you can read the Excel file directly from the URL
url = 'https://github.com/mvlasceanu/RegressionData/raw/main/creditdefault.xls'
df = pd.read_excel(url)

df

	ID	DEFAULT	SEX	EDUCATION	MARRIAGE	AGE	PAY_0	PAY_2	PAY_3	PAY_4	...	BILL_AMT3	BILL_AMT4	BILL_AMT5	BILL_AMT6	PAY_AMT1	PAY_AMT2	PAY_AMT3	PAY_AMT4	PAY_AMT5	PAY_AMT6
0	1	1	2	2	1	24	2	2	-1	-1	...	689	0	0	0	0	689	0	0	0	0
1	2	1	2	2	2	26	-1	2	0	0	...	2682	3272	3455	3261	0	1000	1000	1000	0	2000
2	3	0	2	2	2	34	0	0	0	0	...	13559	14331	14948	15549	1518	1500	1000	1000	1000	5000
3	4	0	2	2	1	37	0	0	0	0	...	49291	28314	28959	29547	2000	2019	1200	1100	1069	1000
4	5	0	1	2	1	57	-1	0	-1	0	...	35835	20940	19146	19131	2000	36681	10000	9000	689	679
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
29995	29996	0	1	3	1	39	0	0	0	0	...	208365	88004	31237	15980	8500	20000	5003	3047	5000	1000
29996	29997	0	1	3	2	43	-1	-1	-1	-1	...	3502	8979	5190	0	1837	3526	8998	129	0	0
29997	29998	1	1	2	2	37	4	3	2	-1	...	2758	20878	20582	19357	0	0	22000	4200	2000	3100
29998	29999	1	1	3	1	41	1	-1	0	0	...	76304	52774	11855	48944	85900	3409	1178	1926	52964	1804
29999	30000	1	1	2	1	46	0	0	0	0	...	49764	36535	32428	15313	2078	1800	1430	1000	1000	1000

30000 rows × 24 columns

# Run a logistic regression predicting DEFAULT (binary variable) as a function of people's education
# one option is to use statsmodels' glm function, and specify the dv is binomial:

Model = smf.glm("DEFAULT ~ EDUCATION", family=sm.families.Binomial(), data=df).fit()
print(Model.summary())

                 Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:                DEFAULT   No. Observations:                30000
Model:                            GLM   Df Residuals:                    29998
Model Family:                Binomial   Df Model:                            1
Link Function:                  Logit   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -15841.
Date:                Sun, 04 Feb 2024   Deviance:                       31682.
Time:                        17:03:24   Pearson chi2:                 3.00e+04
No. Iterations:                     5   Pseudo R-squ. (CS):          0.0007751
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -1.4155      0.035    -39.939      0.000      -1.485      -1.346
EDUCATION      0.0839      0.017      4.848      0.000       0.050       0.118
==============================================================================

# another way of running the analysis above is directly using statsmodels' logit function
# note that the outputs are very similar

Model = smf.logit("DEFAULT ~ EDUCATION", data=df).fit()
print(Model.summary())

Optimization terminated successfully.
         Current function value: 0.528035
         Iterations 5
                           Logit Regression Results                           
==============================================================================
Dep. Variable:                DEFAULT   No. Observations:                30000
Model:                          Logit   Df Residuals:                    29998
Method:                           MLE   Df Model:                            1
Date:                Sun, 04 Feb 2024   Pseudo R-squ.:               0.0007337
Time:                        17:03:24   Log-Likelihood:                -15841.
converged:                       True   LL-Null:                       -15853.
Covariance Type:            nonrobust   LLR p-value:                 1.414e-06
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -1.4155      0.035    -39.939      0.000      -1.485      -1.346
EDUCATION      0.0839      0.017      4.848      0.000       0.050       0.118
==============================================================================

# another way of running the analysis above is directly using statsmodels' logit function
# note that the outputs are very similar

Model = smf.logit("DEFAULT ~ C(EDUCATION)", data=df).fit()
print(Model.summary())

Warning: Maximum number of iterations has been exceeded.
         Current function value: 0.525344
         Iterations: 35
                           Logit Regression Results                           
==============================================================================
Dep. Variable:                DEFAULT   No. Observations:                30000
Model:                          Logit   Df Residuals:                    29993
Method:                           MLE   Df Model:                            6
Date:                Sun, 04 Feb 2024   Pseudo R-squ.:                0.005826
Time:                        17:03:25   Log-Likelihood:                -15760.
converged:                      False   LL-Null:                       -15853.
Covariance Type:            nonrobust   LLR p-value:                 3.392e-37
=====================================================================================
                        coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------------
Intercept           -20.7459   8547.755     -0.002      0.998   -1.68e+04    1.67e+04
C(EDUCATION)[T.1]    19.3111   8547.755      0.002      0.998   -1.67e+04    1.68e+04
C(EDUCATION)[T.2]    19.5787   8547.755      0.002      0.998   -1.67e+04    1.68e+04
C(EDUCATION)[T.3]    19.6557   8547.755      0.002      0.998   -1.67e+04    1.68e+04
C(EDUCATION)[T.4]    17.9383   8547.755      0.002      0.998   -1.67e+04    1.68e+04
C(EDUCATION)[T.5]    18.0680   8547.755      0.002      0.998   -1.67e+04    1.68e+04
C(EDUCATION)[T.6]    19.0642   8547.755      0.002      0.998   -1.67e+04    1.68e+04
=====================================================================================

C:\ALL\AppData\anaconda3\envs\mada_book\Lib\site-packages\statsmodels\base\model.py:607: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "

Because $$y \sim \text{Bernoulli}(p)$$

\[\log\left(\frac{p}{1-p}\right) = \beta_0+\beta_1 x\]

\[ p = \frac{1}{1+\exp(-(\beta_0+\beta_1 x))} \]

And the intercept is the value at which X=0, which means that to get the probability of default (y=1) we need to replace x with 0 in the equation above, and $\beta_0$ with the value of the intercept from the output (in this case $\beta_0$=-1.4155):

1/(1+ np.exp(-(-1.4155)))

0.1953680110786012

Therefore, the probability of default in this example is 19%.

Now let’s see what happens as education increases: a 1 unit increase in education (so when x=1), the probability of default is now calculated by replacing $\beta_0$ with -1.4155 and $\beta_1$ with 0.0839

1/(1+ np.exp(-(-1.4155 + 0.0839)))

0.20889482960957137

So when X=1 the probability of default is 20%.

Interpreting fit quality:

Look at the pseudo-R2 a measure of the proportional log odds improvement of the fitted logistic regression compared to a model which only includes an intercept but no slope.
The values vary from 0 (when the model does not improve the likelihood) to 1 (where the model fits perfectly and the log-likelihood is maximized at 0). Consquently, higher values indicate a better fit.

Interpreting coefficients:

The logistic regression coefficient β associated with a predictor X is the expected change in log odds of having the outcome per unit change in X. So increasing the predictor by 1 unit (or going from 1 level to the next) multiplies the odds of having the outcome by e to the power β
So a unit increase in some areas of the input space might result in a larger increase than a increase in a region closer to 0 or 1.
The rate of change is highest near the inflection or turning point (which is near the mean of the output data) because that is the part that has the highest tangent (i.e., first derivative).

# include multiple predictors

Model = smf.logit("DEFAULT ~ EDUCATION + AGE + MARRIAGE + SEX", data=df).fit()
print(Model.summary())

Optimization terminated successfully.
         Current function value: 0.526979
         Iterations 5
                           Logit Regression Results                           
==============================================================================
Dep. Variable:                DEFAULT   No. Observations:                30000
Model:                          Logit   Df Residuals:                    29995
Method:                           MLE   Df Model:                            4
Date:                Sun, 04 Feb 2024   Pseudo R-squ.:                0.002731
Time:                        17:03:25   Log-Likelihood:                -15809.
converged:                       True   LL-Null:                       -15853.
Covariance Type:            nonrobust   LLR p-value:                 6.938e-18
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -0.8727      0.108     -8.045      0.000      -1.085      -0.660
EDUCATION      0.0780      0.018      4.413      0.000       0.043       0.113
AGE           -0.0011      0.002     -0.661      0.509      -0.004       0.002
MARRIAGE      -0.1099      0.030     -3.723      0.000      -0.168      -0.052
SEX           -0.2027      0.028     -7.133      0.000      -0.258      -0.147
==============================================================================

# look for interactions:
# example: do unmarried men default more than unmarried women (when controlling for eduacation and age)?

Model = smf.logit("DEFAULT ~ EDUCATION + AGE + MARRIAGE*SEX", data=df).fit()
print(Model.summary())

Optimization terminated successfully.
         Current function value: 0.526967
         Iterations 5

                           Logit Regression Results                           
==============================================================================
Dep. Variable:                DEFAULT   No. Observations:                30000
Model:                          Logit   Df Residuals:                    29994
Method:                           MLE   Df Model:                            5
Date:                Sun, 04 Feb 2024   Pseudo R-squ.:                0.002754
Time:                        17:03:25   Log-Likelihood:                -15809.
converged:                       True   LL-Null:                       -15853.
Covariance Type:            nonrobust   LLR p-value:                 2.473e-17
================================================================================
                   coef    std err          z      P>|z|      [0.025      0.975]
--------------------------------------------------------------------------------
Intercept       -0.7590      0.173     -4.375      0.000      -1.099      -0.419
EDUCATION        0.0788      0.018      4.452      0.000       0.044       0.113
AGE             -0.0012      0.002     -0.708      0.479      -0.004       0.002
MARRIAGE        -0.1824      0.091     -1.998      0.046      -0.361      -0.004
SEX             -0.2730      0.088     -3.087      0.002      -0.446      -0.100
MARRIAGE:SEX     0.0455      0.054      0.839      0.401      -0.061       0.152
================================================================================

Logistic regression Example 2#

Also predicting default but now using credit balance

url = "https://raw.githubusercontent.com/Statology/Python-Guides/main/default.csv"
data = pd.read_csv(url)
data

	default	student	balance	income
0	0	0	729.526495	44361.625074
1	0	1	817.180407	12106.134700
2	0	0	1073.549164	31767.138947
3	0	0	529.250605	35704.493935
4	0	0	785.655883	38463.495879
...	...	...	...	...
9995	0	0	711.555020	52992.378914
9996	0	0	757.962918	19660.721768
9997	0	0	845.411989	58636.156984
9998	0	0	1569.009053	36669.112365
9999	0	1	200.922183	16862.952321

10000 rows × 4 columns

data.student.unique()

array([0, 1], dtype=int64)

# Run a logistic regression predicting DEFAULT (binary variable) as a function of people's credit balance
# one option is to use statsmodels' glm function, and specify the dv is binomial:

Model = smf.glm("default ~ student", family=sm.families.Binomial(), data=data).fit()
print(Model.summary())

                 Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:                default   No. Observations:                10000
Model:                            GLM   Df Residuals:                     9998
Model Family:                Binomial   Df Model:                            1
Link Function:                  Logit   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -1454.3
Date:                Sun, 04 Feb 2024   Deviance:                       2908.7
Time:                        17:03:26   Pearson chi2:                 1.00e+04
No. Iterations:                     6   Pseudo R-squ. (CS):           0.001196
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -3.5041      0.071    -49.554      0.000      -3.643      -3.366
student        0.4049      0.115      3.520      0.000       0.179       0.630
==============================================================================

# Run a logistic regression predicting DEFAULT (binary variable) as a function of people's credit balance
# one option is to use statsmodels' glm function, and specify the dv is binomial:

Model = smf.glm("default ~ C(student)", family=sm.families.Binomial(), data=data).fit()
print(Model.summary())

                 Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:                default   No. Observations:                10000
Model:                            GLM   Df Residuals:                     9998
Model Family:                Binomial   Df Model:                            1
Link Function:                  Logit   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -1454.3
Date:                Sun, 04 Feb 2024   Deviance:                       2908.7
Time:                        17:03:26   Pearson chi2:                 1.00e+04
No. Iterations:                     6   Pseudo R-squ. (CS):           0.001196
Covariance Type:            nonrobust                                         
===================================================================================
                      coef    std err          z      P>|z|      [0.025      0.975]
-----------------------------------------------------------------------------------
Intercept          -3.5041      0.071    -49.554      0.000      -3.643      -3.366
C(student)[T.1]     0.4049      0.115      3.520      0.000       0.179       0.630
===================================================================================

#plot logistic regression curve
sns.regplot(x=data.balance, y=data.default, data=data, color='red', scatter_kws={'color': 'gray'}, logistic=True)

# Run a logistic regression predicting DEFAULT (binary variable) as a function of people's credit balance
# one option is to use statsmodels' glm function, and specify the dv is binomial:

Model = smf.glm("default ~ balance", family=sm.families.Binomial(), data=data).fit()
print(Model.summary())

                 Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:                default   No. Observations:                10000
Model:                            GLM   Df Residuals:                     9998
Model Family:                Binomial   Df Model:                            1
Link Function:                  Logit   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -798.23
Date:                Tue, 16 Jan 2024   Deviance:                       1596.5
Time:                        15:09:18   Pearson chi2:                 7.15e+03
No. Iterations:                     9   Pseudo R-squ. (CS):             0.1240
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept    -10.6513      0.361    -29.491      0.000     -11.359      -9.943
balance        0.0055      0.000     24.952      0.000       0.005       0.006
==============================================================================

2. Multinomial Regression#

When the DV has more than 2 options, use a multinomial logistic regression (MNLogit).

Examples:

yes, no, maybe
Democratic, Republican, Independent

Multinomial logistic regression is also called multiclass logistic regression, or softmax regression

\[y \sim \text{Multinomial}(\mathbf{p})\]

\[\mathbf{p} = \left[\frac{e^{f_1}}{\sum_i e^{f_i}},...,\frac{e^{f_K}}{\sum_i e^{f_i}}\right]\]

\[ \mathbf{f}=\boldsymbol{\beta}_0 + \boldsymbol{\beta}_1x \]

\[\boldsymbol{\beta}_0 = [\beta_{0,1}, ... \beta_{0,K-1}, 0], \boldsymbol{\beta}_1 = [\beta_{1,1}, ... \beta_{1,K-1}, 0]\]

# import data downloaded from https://github.com/mvlasceanu/RegressionData/blob/main/data.xlsx
# df2 = pd.read_excel('data.xlsx')

# Or you can read the Excel file directly from the URL
url = 'https://github.com/mvlasceanu/RegressionData/raw/main/data.xlsx'
df2 = pd.read_excel(url)

df2.head()

	Response ID	GENDER	AGE	PARTY	TWITTER	TRUST	RU1	RU2	RU3	RU4	...	Post23	Post24	Post25	Post26	Post27	Post28	Post29	Post30	Post31	Post32
0	R_0cj5dsJg2wfpiuJ	1	18	1	0	95	4.0	26	0	-5	...	69	60	20	58	84	22	42	77	90	71
1	R_0rkhLjwWPHHjnTX	0	19	2	1	76	-5.0	16	3	-1	...	58	82	38	61	36	40	62	68	46	43
2	R_10BMNpjhInMfUeO	1	18	1	1	86	-5.0	-2	5	5	...	35	46	39	65	44	42	53	55	45	35
3	R_120iGR6WlLnbZnI	0	22	1	0	95	23.0	-10	-40	22	...	14	76	20	61	87	82	63	19	97	37
4	R_12qW8cDY0bNlId2	0	19	3	0	76	18.0	-12	1	16	...	17	81	31	83	82	76	43	33	82	47

5 rows × 102 columns

# What is the probability some is a Democrat (PARTY==1), or a Republican (PARTY==2), or an Independent (PARTY==3)?

expr = "PARTY ~ TRUST" # first specify the equation as Outcome ~ Predictor
y, x = dmatrices(expr, df2, return_type='dataframe') # then using the equation create a design matrix
Model = sm.MNLogit(y, x).fit() # then fit the multinomial regression model
print(Model.summary()) # print the summary

Optimization terminated successfully.
         Current function value: 0.837480
         Iterations 6
                          MNLogit Regression Results                          
==============================================================================
Dep. Variable:                  PARTY   No. Observations:                  200
Model:                        MNLogit   Df Residuals:                      196
Method:                           MLE   Df Model:                            2
Date:                Tue, 16 Jan 2024   Pseudo R-squ.:                 0.04317
Time:                        15:09:19   Log-Likelihood:                -167.50
converged:                       True   LL-Null:                       -175.05
Covariance Type:            nonrobust   LLR p-value:                 0.0005229
==============================================================================
   PARTY=2       coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      3.0955      1.513      2.046      0.041       0.130       6.061
TRUST         -0.0579      0.018     -3.186      0.001      -0.093      -0.022
------------------------------------------------------------------------------
   PARTY=3       coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      2.7394      1.223      2.240      0.025       0.343       5.136
TRUST         -0.0423      0.014     -2.974      0.003      -0.070      -0.014
==============================================================================

# output interpretation
# when trust in science goes up, the probability of being in Party==2 goes down because the coefficient of "TRUST" is negative
# when trust in science goes up, the probability of being in Party==3 also goes down because the coefficient of "TRUST" is negative

# when trust in science goes up, the probability of being in Party==1 has to go up because the other 2 go down and the 3 of them have to always sum to 1.

# For zero trust in science, what is the probability of being [Democrat, Republican, Independent]?
# Plug in the intercepts for each category in the formula below
# note the intercept for the base category (in this case "Democrats" as they are alphabetically first) is always 0

_sum = np.exp(0)+np.exp(3.0955)+np.exp(2.7394)
[np.exp(0)/_sum, np.exp(3.0955)/_sum, np.exp(2.7394)/_sum]

[0.025922866617322432, 0.572850892405553, 0.4012262409771245]

# For X trust in science, what is the probability of being [Democrat, Republican, Independent]?
# First, choose a level of the IV (here, trust in science)
# then plug in the intercept and slope from the regression output in the formula below

trust = 80 # This value plugs in below

_sum = np.exp(0)+np.exp(3.0955-0.0579*trust)+np.exp(2.7394-0.0423*trust)
[np.exp(0)/_sum, np.exp(3.0955-0.0579*trust)/_sum, np.exp(2.7394-0.0423*trust)/_sum]

[0.5747109264810433, 0.12363914201115143, 0.3016499315078052]

3. Poisson Regression#

Poisson Regression is another generalized linear model.
It is also called a log-linear model.
Poisson Regression is used when the DV has a Poisson distribution (e.g., count data)
Poisson regression models are generalized linear models with the logarithm as the (canonical) link function, and the Poisson distribution function as the assumed probability distribution of the response.
Negative binomial regression is a popular generalization of Poisson regression (used when variance of count data is very large).
The traditional negative binomial regression model is based on the Poisson-gamma mixture distribution.

A Formal Specification of the Poisson Regression Model: For the ith observation in the data set denoted by $y_i$ corresponding to the row of regression variables x_i, the probability of observing the count y_i is Poisson distributed as per the following PMF, where the mean rate λ_i for the ith sample is given by the exponential link function

\[y \sim \text{Poisson}(\lambda)\]

\[\log(\lambda) = \beta_0+\beta_1 x\]

\[\lambda = e^{\beta_0+\beta_1 x}= e^{\beta_0}e^{\beta_1 x}\]

Example of Poisson regression#

What predicts how many bikes cross the Brooklyn Bridge in a given day

# import data downloaded from https://github.com/mvlasceanu/RegressionData/blob/main/bike.xlsx
# data source: NYC Open Data: Bicycle Counts for East River Bridges Raw
# df = pd.read_excel('bike.xlsx')

# Or you can read the Excel file directly from the URL
url = 'https://github.com/mvlasceanu/RegressionData/raw/main/bike.xlsx'
df = pd.read_excel(url)

df

	Date	HIGH_T	LOW_T	PRECIP	BB_COUNT
0	2017-04-01	46.0	37.0	0.00	606
1	2017-04-02	62.1	41.0	0.00	2021
2	2017-04-03	63.0	50.0	0.03	2470
3	2017-04-04	51.1	46.0	1.18	723
4	2017-04-05	63.0	46.0	0.00	2807
...	...	...	...	...	...
209	2017-10-27	62.1	48.0	0.00	3150
210	2017-10-28	68.0	55.9	0.00	2245
211	2017-10-29	64.9	61.0	3.03	183
212	2017-10-30	55.0	46.0	0.25	1428
213	2017-10-31	54.0	44.0	0.00	2727

214 rows × 5 columns

# Test whether fewer people bike on the Brooklyn Bridge on rainy days

expr = "BB_COUNT ~ PRECIP"
y, x = dmatrices(expr, df, return_type='dataframe')
Model = sm.GLM(y, x, family=sm.families.Poisson()).fit()
print(Model.summary())

                 Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:               BB_COUNT   No. Observations:                  214
Model:                            GLM   Df Residuals:                      212
Model Family:                 Poisson   Df Model:                            1
Link Function:                    Log   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -21245.
Date:                Tue, 16 Jan 2024   Deviance:                       40425.
Time:                        15:09:19   Pearson chi2:                 3.84e+04
No. Iterations:                     6   Pseudo R-squ. (CS):              1.000
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      7.9751      0.001   5769.063      0.000       7.972       7.978
PRECIP        -0.9289      0.007   -136.083      0.000      -0.942      -0.916
==============================================================================

# calculate e to the power of the intercept coefficient
# this number is the average number of bikes on the bridge when X=0 (precipitation = 0, so not raining)
np.exp(7.97)

2892.857364220396

This means, when it’s not raining, the average number of bikes on the bridge is 2892.

# calculate e to the power of the coefficient (in this example the coefficient is -0.92)
# this number is used in interpreting the relationship between the IV and DV

np.exp(-0.92)

0.39851904108451414

Interpretation:

The Poisson regression coefficient β associated with a predictor X is the expected change, on the log scale, in the outcome Y per unit change in X. So holding all other variables in the model constant, increasing X by 1 unit (or going from 1 level to the next) multiplies the rate of Y by e to the power β
in our example, a one unit increase in precipitation is associated with (e to the power -0.92, which equals 0.39) 0.39 times fewer bikes on Brooklyn Bridge. I said fewer because the coefficient is negative in this example.

# if you want to think about it in terms of percent change, calculate the percent change using the formula:
# percent change = (new-old)/old
# in our case new = exp(beta0)*exp(beta1)
# and old = exp(beta0)
# therefore, percent change of bikes associated with a unit increase in percipitation is:
# (exp(beta0)*exp(beta1) - exp(beta0)) / exp(beta0) = exp(beta1) - 1

np.exp(-0.92) - 1

-0.6014809589154859

Thus, raining is associated with a 60% decrease in biking on Brooklyn Bridge.

4. Ordinal Regression#

Ordinal regression is used when the outcome variable (DV) is ordinal.

Examples:

likert measures: - Strongly Disagree – Slightly Disagree – Slighty Agree – Strongly Agree - Unlikely – Somewhat likely – Likely

Ordinal regression is also called ranking learning or ordinal classification. Here, we will run an ordered logit as an example.

\[\Pr(y\le k) \sim \text{Bernoulli}(p)\]

\[ p = \frac{1}{1+e^{-(\theta_k - \beta_1 x)}} \]

Note the minus $\beta_1 x$ as well as the threshold $\theta_k$ for the outcome option $k$ (also called levels). This is a cumulative probability that a datapoint is below the k-th level, so the probability that a datapoint is in the k-th level is

\[\Pr(y= k) = \Pr(y\le k) - \Pr(y\le k-1)\]

from statsmodels.miscmodels.ordinal_model import OrderedModel

# get data
# This dataset is about the probability for undergraduate students to apply to graduate school given three exogenous variables:
# 1. "gpa" which means grade point average in college
# 2. "pared" which indicates if at least one parent went to graduate school
# 3. "public" which indicates if the current undergraduate institution of the student is public or private

url = "https://stats.idre.ucla.edu/stat/data/ologit.dta"
data_student = pd.read_stata(url)
data_student

	apply	pared	public	gpa
0	very likely	0	0	3.26
1	somewhat likely	1	0	3.21
2	unlikely	1	1	3.94
3	somewhat likely	0	0	2.81
4	somewhat likely	0	0	2.53
...	...	...	...	...
395	unlikely	0	0	3.70
396	unlikely	0	0	2.63
397	somewhat likely	0	0	2.25
398	somewhat likely	0	0	3.26
399	very likely	0	0	3.52

400 rows × 4 columns

data_student['apply'].hist()

<Axes: >

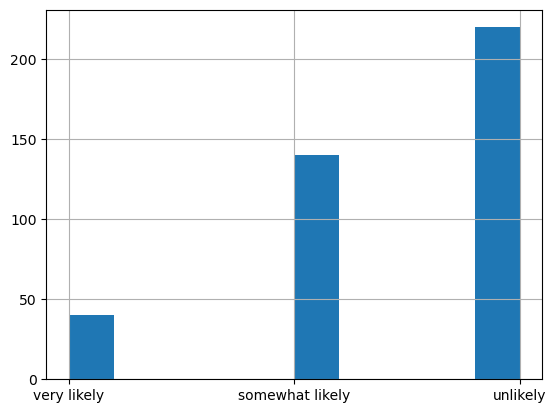
_images/84ab74b2e678667f040c76ac0fbe53412e2ffd26db1440e3d4f1cb7e88a4dc34.png

# Run the model using 'gpa' to predict probability of 'apply'

model = OrderedModel(data_student['apply'], data_student['gpa'], distr='logit') # give the DV, then the IV
result = model.fit(method='bfgs', disp=False)
print(result.summary())

                             OrderedModel Results                             
==============================================================================
Dep. Variable:                  apply   Log-Likelihood:                -366.30
Model:                   OrderedModel   AIC:                             738.6
Method:            Maximum Likelihood   BIC:                             750.6
Date:                Tue, 16 Jan 2024                                         
Time:                        15:09:20                                         
No. Observations:                 400                                         
Df Residuals:                     397                                         
Df Model:                           1                                         
===============================================================================================
                                  coef    std err          z      P>|z|      [0.025      0.975]
-----------------------------------------------------------------------------------------------
gpa                             0.7249      0.249      2.908      0.004       0.236       1.213
unlikely/somewhat likely        2.3749      0.757      3.137      0.002       0.891       3.859
somewhat likely/very likely     0.7056      0.080      8.836      0.000       0.549       0.862
===============================================================================================

# Output interpretation:
# As GPA increases, the expected level of the outcome variable significantly increases (p=0.004).

# The unlikely/somewhat likely and somewhat likely/very likely are not the class thresholds directly;
# postprocess those with provided functions:
number_of_levels = 3
model.transform_threshold_params(result.params[-(number_of_levels-1):])

array([      -inf, 2.37485065, 4.39990038,        inf])

# Probabilities of [unlikely, somewhat likely, very likely] to apply to grad school:
gpa = 4.0

# Probability of "unlikely to apply to grad school"
prob = [1/(1+np.exp(-(2.3749 - 0.7249*gpa)))]
# Probability of "somewhat likely to apply to grad school" = Probability of "at most somewhat likely to apply to grad school" MINUS "unlikely"
prob.append(1/(1+np.exp(-(4.39990038 - 0.7249*gpa))) - sum(prob))
# Probability of "very likely to apply to grad school" = 1 MINUS ("unlikely" + "somewhat likely")
prob.append(1 - sum(prob))
# We subtract `sum(prob)` from each subsequent item because of the _cumulative probabilities_ defined above.

prob

[0.3717538748879268, 0.445865397643395, 0.18238072746867817]

# get model predictions for dataset
pred = result.model.predict(result.params)
preddf = pd.concat((data_student[["gpa"]], pd.DataFrame(pred, columns=["Unlikely", "SomewhatLikely", "VeryLikely"])), axis="columns")

#transform the datafram from wide format to long format using Panda's melt function
preddf2 = pd.melt(
    preddf.loc[:, ["Unlikely", "SomewhatLikely", "VeryLikely", "gpa"]],
    id_vars=["gpa"],
    var_name="Outcome",
    value_name="Likelihood"
)
preddf2

	gpa	Outcome	Likelihood
0	3.26	Unlikely	0.502943
1	3.21	Unlikely	0.512002
2	3.94	Unlikely	0.381983
3	2.81	Unlikely	0.583696
4	2.53	Unlikely	0.632028
...	...	...	...
1195	3.70	VeryLikely	0.152144
1196	2.63	VeryLikely	0.076316
1197	2.25	VeryLikely	0.059026
1198	3.26	VeryLikely	0.115391
1199	3.52	VeryLikely	0.136066

1200 rows × 3 columns

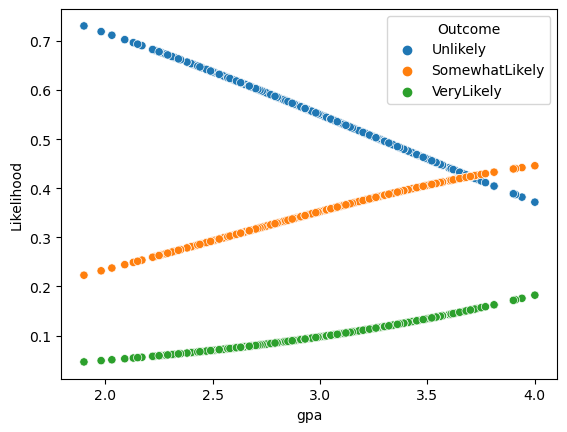
sns.scatterplot(data=preddf2, x="gpa", y="Likelihood", hue="Outcome")

<Axes: xlabel='gpa', ylabel='Likelihood'>

_images/ed3eb7555b2a18f831f0f87667232b5404ca792f4b4cfb466d421508f4380767.png